Blog

Parin Sir > Quantitative Aptitude (Maths) > Fundamental (Numbers) > NUMBERS Examples

NUMBERS Examples

July 11, 2019
Category: Quantitative Aptitude (Maths) Fundamental (Numbers)

No Comments

NUMBERS

Examples :

(1) Evaluate : 25 – | – 8 | – | 7 | + | – 31 |.

Soln. 25 – | – 8 | – | 7 | + | – 31 | = 25 – 8 – 7 + 31 = 41

(2) Find the value of i¹⁸.

Soln. i¹⁸ = $\left ( i^{2} \right )^{9}$ = $\left ( -1 \right )^{9}$ = – 1

(3) If [n] denotes the greatest integer < n, and (n) denotes the smallest integer > n where n is any real number, find $\left ( 4\frac{8}{9} \right )$ – $\left [ 4\frac{8}{9} \right ]$ .

Soln. $\left ( 4\frac{8}{9} \right )$ – $\left [ 4\frac{8}{9} \right ]$ = 5 – 4 = 1.

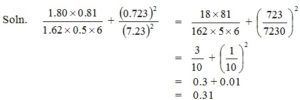
(4) Simplify : $\frac{1.80\times 0.81}{1.62\times0.5\times 6}+\frac{(0.723)^{2}}{(7.23)^{2}}$ .

(5) Simplify : 1.8 + 2 $\sqrt{5}$ + 3 $\sqrt{3}$ + 2.8 + 5 $\sqrt{5}$

Soln. 1.8 + 2 $\sqrt{5}$ + 3 $\sqrt{3}$ + 2.8 + 5 $\sqrt{5}$ = 4.6 + 3 $\sqrt{3}$ + 7 $\sqrt{5}$

(6) Simplify : (2 + 3 $\sqrt{3}$ ) (1 + 2 $\sqrt{3}$ ).

Soln. (2 + 3 $\sqrt{3}$ ) (1 + 2 $\sqrt{3}$ ) = 2 + 4 $\sqrt{3}$ + 3 $\sqrt{3}$ + 6 $\times\sqrt{3\times 3}$ = 20 + 7 $\sqrt{3}$

(7) There are three tanks of volumes 980 m³, 490 m³ and 700 m³ respectively. If they have to be filled up using a bucket, what could be the maximum volume of the bucket ? (The bucket should always be full.)

Soln. Since we have to fill up the tank, volume of the bucket that we select must exactly divide each of the given volume. The only number which would divide each of the above values exactly would be the Highest Common Factor of the numbers.

980 = 70 $\times$ 14; 490 = 70 $\times$ 7; 700 = 70 $\times$ 10

$\therefore$ HCF = 70.

Hence, maximum volume of the bucket is 70 m³.

(8) Simplify : 1 $\times$ 1 + 1 $\div$ 1 – 1

Soln. 1 $\times$ 1 + 1 $\div$ 1 – 1 = 1 $\times$ 1 + 1 – 1 = 1 + 1 – 1 = 2 – 1 = 1.

(9) Simplify : ( $\overline{7-5}$ + 3) $\times$ 4 $\div$ 5 + 3

Soln. ( ( $\overline{7-5}$ + 3) $\times$ 4 $\div$ 5 + 3 = (2 + 3) $\times$ 4 $\div$ 5 + 3 = 5 $\times$ $\frac{4}{5}$ + 3 = 4 + 3 = 7 + 3

(10) Simplify : 0.8 $\div$ 0. $\overline{4}$ 0. of $\frac{9}{5}$ + 90

Soln.

(11) What least number must be added to 16759 to get a number exactly divisible by 37 ?

Soln. On dividing 16759 by 37, the remainder is 35.

$\therefore$ The number to be added = ( 37 – 35 ) = 2.

(14) Find a + b, if 1938a5b is divisible by 33 ( i.e. by 3 and 11 both ).

Soln. Sum of digits = 1 + 9 + 3 + 8 + a + 5 + b = 26 + a + b is divisible by 3

$\therefore$ a + b could be 1, 4, 7, 10, 13 or 16

Also ( 1 + 3 + a + b ) – ( 9 + 8 + 5 ) = 0 or multiple of 11.

$\therefore$ ( 4 + a + b ) – ( 22 ) = a + b – 18 = 0 or multiple of 11. ( i.e. $\pm$ 11, $\pm$ 22, $\pm$ 33 )

$\therefore$ a + b = 7 ( by substituting the different values of a + b in above equation ).

(15)

What could be the maximum value of Q in the following equation ?

7P9 + 3R8 + 2Q7 = 1314

Soln. We may analyze the given equation as shown :

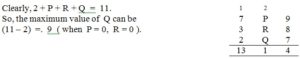
(16) Find the unit’s digit in the product (5327)¹⁵³ (143)⁷².

Soln. First of all divide the index by 4 and find out its remainder.

( Replace the remainder 4 by 1 and others remain as they are. )

(17) Find the unit’s digit in (784)¹⁰² + (784)¹⁰³.

Soln. First of all divide the index by 4 and find out its remainder.

( Replace the remainder 4 by 1 and others remain as they are. )

(18) Find the remainder when 2³⁵ is divided by 5.

Soln. Unit digit of 2³⁵ = 2³ = 8

Now, 8 when divided by 5, gives 3 as remainder.

Hence, 2³⁵ when divided by 5, gives 3 as remainder.

(19) What least value must be assigned to * so that the number 383*1386 is divisible by 9 ?

Soln. Sum of digits = ( 3 + 8 + 3 + * + 1 + 3 + 8 + 6 ) = (32 + *).

For ( 32 + * ) to be divisible by 9, * must be replaced by 4.

Hence, the digit in place of * must be 4.

(20) Which digits should come in place of * and # if the number 35264*# is divisible by both 8 and 5 ?

Soln.

Since the given number is divisible by 5, so 0 or 5 must come in place of # . But, a number ending with 5 is never divisible by 8. So, 0 will replace #.

Now, the number formed by the last three digits is 4*0, which becomes divisible by 8, if * is replaced by 0 or 4.

Hence, digits in place of * = 0 or 4 and # = 0.

(21) What least number must be added and subtract to 3000 to obtain a number exactly divisible by 19 ?

Soln. On dividing 3000 by 19, we get 17 as a remainder.

(22) Find the number which is nearest to 3115 and is exactly divisible by 23.

Soln. On dividing 3105 by 23, we get 10 as a remainder.

(23) A number when divided by 437 gives a remainder 47. When the same number is divided by 19, what would be the remainder ?

Soln.

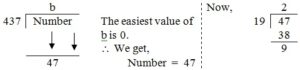
$\therefore$ On dividing 47 by 19 we get the remainder 9.

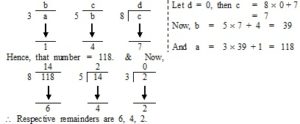
(24) A number being successively divided by 3, 5 and 8 leaves remainders 1, 4 and 7 respectively. Find the respective remainders if the order of divisors be reversed.

Soln.