Blog
Combination
- June 5, 2020
- Category: Combination
☼ COMBINATION : When we have to choose a certain number of objects from a given set of objects in such a way that the order of selection is not important, the selection is known as a combination. Consider the following example.
e.g. There were three persons in a meeting. Each person shook hands with every other person. Find the total number of ways this happened.
Soln. Let, the persons were A, B and C. They shook hand in the way : A B, A
C, B
C
i.e. Only three ways are possible.
In the above example, 2 persons were needed from a group of 3 persons for shake hand such a way that the order of the arrangements is not important.
( i.e. A B & B
A are same. )
Now, if there were n = 3 persons and r = 2 persons were to be selected, then we could make the selection in = 3 ways.
This can also be written as =
=
Number of combinations =
=
■ Number of permutations = Number of combinations r ! ( i.e.
=
r ! )
■ =
=
; 0
r
n
■ =
= 56,
=
= 792,
= 5,
= 1 =
■ The distinct symbols for combination = =
=
■ We can find the distinct value of by Pascal triangle also
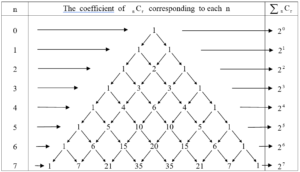
■ =
&
+
=
e.g. (i) In a window there are m vertical and n horizontal bars. Find the number of rectangles formed. (m, n 2)
Soln. By selecting 2 vertical bars and 2 horizontal bars a rectangle can be formed.
The required no. of rectangles are =
=
=
(ii) Find the number of diagonals in a polygon of n sides (or n vertices). (n 3 )
Soln. Here, no. of sides of a polygon = n
& Total no. of line-segment joining any two points from given
n points =
The required no. of diagonals are =
– No. of sides
=
= [(n – 1) – 2]
=
(iii) In how many ways can 3 mangoes and 2 apples be selected from 7 mangoes and 4 apples to form a basket of 5 fruits ?
Soln. 3 mangoes can be selected from 7 mangoes in ways and 2 apples can be selected from 4 apples in
ways.
Total number of ways =
= 35 6 = 210
