☼ PAIRS OF  ANGLES  :  

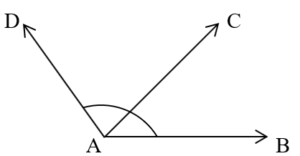
■ Adjacent  angles  :   Consider two angles BAC  and  CAD  with the same vertex A and  the arm AC  common to them. Two such angles with the same vertex, one arm common are called adjacent angles. Or, we can say that two angles in a plane are adjacent angles if they have common vertex, a common arm and their interiors do not overlap. Thus, in the figure, BAC and  CAD  are adjacent angles.

■ Linear  pair  :

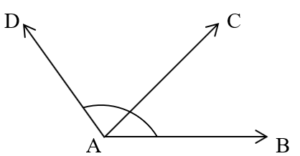
The adjacent pair of  angle whose sum is 180⁰ is called a linear pair.

Here,  mBAC  +  mCAD  =  180⁰.

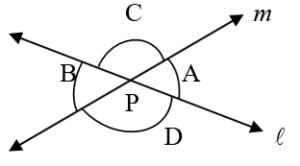
■ Vertically opposite angles  :   Two angles formed by two intersecting lines having no common arm are called vertically opposite angles. Thus, from the figure  A  and  B,  and  C  and  D  are vertically opposite angles. These vertically opposite angles are equal.

i.e., mA  =  mB   and   mC  =  mD.

Also sum of  angles around a point is 360^c.

i.e.,  mA + mB + mC + mD  =  360⁰.

■ Complementary  angles  :   If  the sum of  two angles is 90⁰, then the angles are called complementary angles and each angle is called a complement of  the other.

e.g., angles  60⁰ and  30⁰ are complementary angles. The angles of  60⁰ is the complement of  the angle of  30⁰ and the angle of  30⁰ is the complement of  the angle of  60⁰.

■ Supplementary  angles  :   If the sum of  two angles is 180⁰, then the angles are called supplementary angles and each of  them is called the supplement of  the other.

e.g.,, angles of  70⁰ and  110⁰ are supplementary angles. The angle of  70⁰ is the supplement of  the angle of  110⁰ and the angle of  110⁰ is the supplement of  the angle of  70⁰.

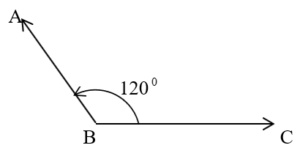
Note that the angles of  a linear pair are supplementary. Is it true that supplementary angles always form a linear pair ?  No.

In  the figures,  ABC + DEF  =  120⁰ + 60⁰  =  180⁰.  But they are not adjacent angles, and hence do not form a linear pair.

Click to next topic