Blog
Parin Sir > Quantitative Aptitude (Maths) > Circle > Some Important Results > Some Important Results
Some Important Results
- August 8, 2020
- Category: Some Important Results
No Comments
☼ Some Important Results :
- The perpendicular drawn through the centre of a circle on a chord bisects the chord.
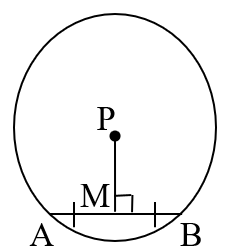
In the adjoining figure,
is a chord of a circle ⊙ ( P, r ) and
, then
bisects
at M.
i.e. M is the mid–point of .
Some important results :
- The perpendicular bisector of a chord of a circle, lying in the plane of the circle, passes through the centre of the circle.
- Three distinct collinear points cannot be the points on the same circle.
- One and only one circle passes through three distinct non–collinear points.
- If two chords of a circle bisect each other, both of them are diameters of the circle.
- In the same circle, if two chords other than a diameter are given, the distance of the longer chord from the centre is less than the distance of the smaller chord from the centre.
- If two distinct points are on two circles, then it is said that both the circles intersect and those points are called their points of intersection.
- Two distinct circles cannot intersect each other in more than two distinct points.
- If one and only one point is on two circles, then it is said that both the circles touches and that point is called their point of tangent.
- In the same circle ( or in congruent circles ) congruent chords are equidistant from the centre ( centres ) of the circle ( circles ).
- If
and
are congruent chords of ⊙ ( P, r ), then AP bisects
BAC.
Common chord : If two distinct circles intersect each other in distinct points A and B, then is called the common chord of the two circles.
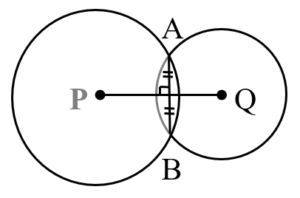
If two distinct circles have a common chord, it is always unique i.e., two distinct circles cannot have more than one common chord.
↦ If is a common chord of ⊙ (P, r) and ⊙ (Q, r2), then
bisects
perpendicularly.
