Blog
Circle and its tangent
- August 8, 2020
- Category: Circle and its tangent
☼ Circle and its tangent :
↦ Three collinear points cannot lie on a circle.
↦ If a line in the plane of a circle has common point with the circle, then there are two alternatives :
- The line intersects the circle in two distinct points. Such a line is called a secant.
- The line intersects the circle in one and only one point. Such a line is called a tangent of the circle at that point.
Tangent : A line in the plane of a circle intersecting the circle at one and only one point is called a tangent of the circle at that point and the point of intersection is called the point of contact.
↦ A tangent of a circle is perpendicular to the radius drawn through the point of contact.
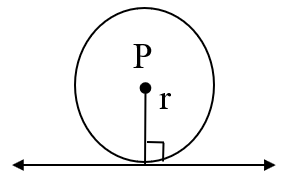
↦ Only one tangent can be drawn to a circle through a point on the circle.
↦ Two tangents to a circle can be drawn from a point lying in the exterior of the circle.
In this case,
 .
.
- PT1 = PT2
bisects
at right angles.
is the bisector of ∠ T1PT2 and CP is the bisector of T1CT2.
Relation between a line and a circle :
If a line and a circle are given in the same plane and the perpendicular from the centre of the circle on the line is drawn, then we note the following :
- If the foot of the perpendicular is in the exterior of the circle, then each point of that line is in the exterior of the circle.
- If the foot of the perpendicular is on the circle, then the line intersects the circle in one and only one point.
- If the foot of the perpendicular is in the interior of the circle ( or the line passes through the centre of the circle ), then the line intersects the circle in exactly two points at equal distance from the foot of the perpendicular ( or the centre )

- The measure of an angle made by a chord of a circle with the tangent touching the circle at one of the end-points of the chord is equal to the measure of an angle made by the chord in the alternate segment.
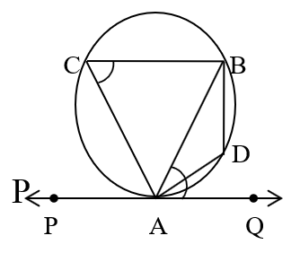
In the adjoining figure :
m∠ BAQ = m∠ACB
and similarly, m∠BAP = m∠ADB
● If the lines containing two distinct chords intersect each other ( in the interior or the exterior of the circle ), then the area of the rectangle formed by the segments of one chord is equal to the area of the rectangle formed by the segments of the other chord.

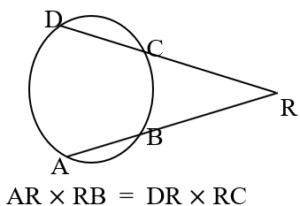
● If the tangent at a point T of a circle and a secant
of the circle, passing through points A and B of the circle, intersect each other at a point P in the exterior of the circle, then
=
.
● Two circles touching each other :
↦ If two distinct circles ( lying in the same plane ) touch a line at the same point, then these circles are said to touch each other at that point and that line is called a common tangent of those circles and that point is called their common point of contact.

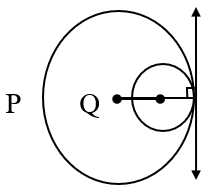
↦ If the centres of two circles, touching each other lie in the opposite half planes of their common tangent, then we say that these two circles touch each other externally and if their centres lie in the same half-plane of their common tangent then we say that these two circles touch each other internally.
↦ The common point of contact of two circles touching each other is on the line joining the centres of the circles.
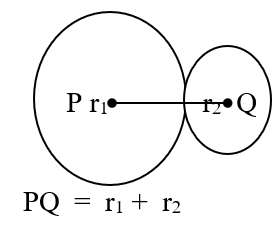
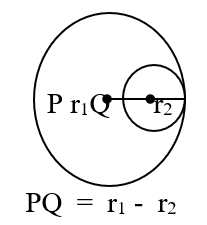
Distance between centers of circles touching each other :
- The distance between the centers of two circles touching each other externally is equal to the sum of their radii.
- The distance between the centers of two circles touching each other internally is equal to the positive difference of their radii.
Cyclic quadrilateral : A quadrilateral having all its four vertices on the same circle is a called a cyclic quadrilateral.
↦ The circle passing through all the four vertices of a quadrilateral is called the circumcircle of the quadrilateral.
↦The oppositeangles of a cyclic quadrilateral are supplementary.
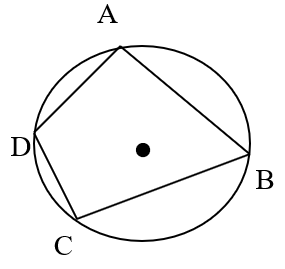
i.e. In the cyclic ABCD,
m∠A + m∠C = 180
m∠B + m∠= 180
↦A parallelogram inscribed in a circle is a rectangle.
↦A rhombus inscribed in a circle is a square.
↦ If a trapezium is inscribed in a circle, its non–parallel sides are congruent, its diagonals are congruent and the angles on parallel sides are congruent, i.e., in cyclic trapezium ABCD, if AB || CD, then AD ≅ BC, , ∠A ≅∠B and ∠C ≅∠D.
In–radius of a triangle ( radius of the In–circle of a triangle )
↦ If r is the in–radius of Δ ABC, then
the area of ΔABC = r ( AB + BC + CA )
= r ( Perimeter of ΔABC )
↦ If ΔABC is a right angled triangle and r is its in–radius, then
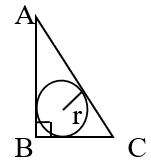
that is
↦ In above diagramme, ΔABC is called circumscribed about a circle.
↦ A parallelogram circumscribed about a circle is a rhombus.
↦ A rectangle circumscribed about a circle is a square.
