Blog

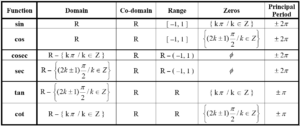
Parin Sir > Quantitative Aptitude (Maths) > T-Ratios & Identities > Domain Range Co-domain Zeros and Principal Period of Trigo Functions : - > Domain Range Co-domain Zeros and Principal Period of Trigo Functions : -

Domain Range Co-domain Zeros and Principal Period of Trigo Functions : -

August 11, 2020
Category: Domain Range Co-domain Zeros and Principal Period of Trigo Functions : -

No Comments

☼ Domain, Range, Co-domain, Zeros and Principal Period of Trigo. Functions : –

First Quadrant

sin $\left(\frac{\pi}{2}-\theta\right)$ = cos θ sin ( $2\pi+\theta$ ) = sin θ

cos $\left(\frac{\pi}{2}-\theta\right)$ = sin θ cos ( $2\pi+\theta$ ) = cos θ

tan $\left(\frac{\pi}{2}-\theta\right)$ = cot θ tan ( $2\pi+\theta$ ) = tan θ

Second Quadrant

sin $\left(\frac{\pi}{2}+\theta\right)$ = cos θ sin ( $\pi-\theta$ ) = sin θ

cos $\left(\frac{\pi}{2}+\theta\right)$ = – sin θ cos ( $\pi-\theta$ ) = – cos θ

tan $\left(\frac{\pi}{2}+\theta\right)$ = – cot θ tan ( $\pi-\theta$ ) = – tan θ

Third Quadrant

sin $\left(\frac{3\pi}{2}-\theta\right)$ = – cos θ sin ( $\pi+\theta$ ) = – sin θ

cos $\left(\frac{3\pi}{2}-\theta\right)$ = – sin θ cos ( $\pi+\theta$ ) = – cos θ

tan $\left(\frac{3\pi}{2}-\theta\right)$ = cot θ tan ( $\pi+\theta$ ) = tan θ

Fourth Quadrant

sin $\left(\frac{3\pi}{2}+\theta\right)$ = – cos θ sin ( $2\pi-\theta$ ) = – sin θ

cos $\left(\frac{3\pi}{2}+\theta\right)$ = sin θ cos ( $2\pi-\theta$ ) = cos θ

tan $\left(\frac{3\pi}{2}+\theta\right)$ = – cot θ tan ( $2\pi-\theta$ ) = – tan θ

* Some Results : –

1) $\theta = \frac{180}{\pi} \times \alpha$ Where, $\theta$ = an angle measured in degree.

$\alpha = \frac{\pi}{180} \times \theta$ $\alpha$ = a length of an arc measured in radian.

2) sin²α – sin²β = cos² β – cos² α = sin (α + β) sin (α – β)

cos²α – sin² β = cos² β – sin² α = cos (α + β) cos (α – β)

3) Range of f (α) = cos α + b sin β is $\left[-r,r\right]$ , where r = $\sqrt{a^2+b^2}$

4) 2 sin α cos β

= sin( $\alpha+\beta$ ) + sin ( $\alpha-\beta$ )

2 cos α sin β

= sin( $\alpha+\beta$ ) – sin ( $\alpha-\beta$ )

2 cos α cos β

= cos( $\alpha+\beta$ ) + cos ( $\alpha-\beta$ )

2 sin α sin β

= cos ( $\alpha-\beta$ ) – cos( $\alpha+\beta$ )

= – cos ( $\alpha+\beta$ ) + cos( $\alpha-\beta$ )

sin C + sin D = 2 sin $\left(\frac{C+D}{2}\right)$ cos $\left(\frac{C-D}{2}\right)$

sin C – sin D = 2 cos $\left(\frac{C+D}{2}\right)$ sin $\left(\frac{C-D}{2}\right)$

cos C + cos D = 2 cos $\left(\frac{C+D}{2}\right)$ cos $\left(\frac{C-D}{2}\right)$

cos C – cos D = – 2 sin $\left(\frac{C+D}{2}\right)$ sin $\left(\frac{C-D}{2}\right)$

5) sin 2 α = 2 sin α cos α

= $\frac{2tan{\alpha}}{1+{tan}^2{\alpha}}$ cos 2 α = cos² α – sin² α

= 2 cos² α – 1

= 1 – 2sin² α

= $\frac{1-{tan}^2{\alpha}}{1+{tan}^2{\alpha}}$

tan 2 α = $\frac{2tan{\alpha}}{1-{tan}^2{\alpha}}$

6) sin² α = $\frac{1-cos{2}\alpha}{2}$

2 sin² α = 1 – cos 2 α cos² α = $\frac{1+cos{2}\alpha}{2}$

2 cos² α = 1 + cos 2

tan² α = $\frac{1-cos{2}\alpha}{1+cos{2}\alpha}$

7) sin 3 α = 3 sin α – 4 sin³ α

cos 3 α = 4 cos³ α – 3 cos α

tan 3 α = $\frac{3tan{\alpha}-{tan}^3{\alpha}}{1-3{tan}^2{\alpha}}$

8) sin 15⁰ = cos 75⁰ = $\frac{\sqrt3-1}{2\sqrt2}$

tan 15⁰ = cot 75⁰ = 2 – $\sqrt3$

sin 18⁰ = cos 72⁰ = $\frac{\sqrt5-1}{4}$

sin 36⁰ = cos 54⁰ = $\frac{\sqrt{10-2\sqrt5}}{4}$

sin 75⁰ = cos 15⁰ = $\frac{\sqrt3+1}{2\sqrt2}$

tan 75⁰ = cot 15⁰ = 2 + $\sqrt3$

sin 72⁰ = cos 18⁰ = $\frac{\sqrt{10+2\sqrt5}}{4}$

sin 54⁰ = cos 36⁰ = $\frac{\sqrt5+1}{4}$

9) tan 22 ${\frac{1}{2}}^0$ = cot 67 ${\frac{1}{2}}^0$ = $\sqrt2 - 1$

sin 22 ${\frac{1}{2}}^0$ = cos 67 ${\frac{1}{2}}^0$ = $\frac{\sqrt{2-\sqrt2}}{2}$

tan 67 ${\frac{1}{2}}^0$ = cot 22 ${\frac{1}{2}}^0$ = $\sqrt2$ + 1

sin 67 ${\frac{1}{2}}^0$ = cos 22 ${\frac{1}{2}}^0$ = $\frac{\sqrt{2+\sqrt2}}{2}$

10) sin-1 (– x ) = – sin-1 x ; $\left|x\right| \leq 1$

cosec-1 (– x ) = – cosec-1 x ; $\left|x\right| \geq 1$

tan-1 (– x ) = – tan-1 x ; $x \in R$

cos-1 (– x ) = π – cos-1 x ; $\left|x\right| \le 1$

sec-1 (– x ) = π – sec-1 x ; $\left|x\right| \geq 1$

cot-1 (– x ) = π – cot-1 x ; $x \in R$

11) cosec^-1 x = sin^-1 $\frac{1}{x}$ ; $\left|x\right| \geq 1$

sec^-1 x = cos^-1 $\frac{1}{x}$ ; $\left|x\right| \geq 1$

cot^-1x = tan^-1 $\frac{1}{x}$ ; x > 0

= π + tan^-1 $\frac{1}{x}$ ; x < 0

12) sin^-1x + cos^-1x = $\frac{\pi}{2}$ ; $\left|x\right| \le 1$

sec^-1x + cosec^-1x = $\frac{\pi}{2}$ ; $\left|x\right| \geq 1$

13) If x > 0 and y > 0, then

tan^-1x + tan^-1y = tan^-1 $\frac{x+y}{1-xy}$ ; xy < 1

tan^-1x + tan^-1y = \pi + tan^-1 $\frac{x+y}{1-xy}$ ; xy > 1

tan^-1x + tan^-1y = $\frac{\pi}{2}$ ; xy = 1

tan^-1x – tan^-1y = tan^-1 $\frac{x-y}{1+xy}$

14) sin^-1x = cos^-1 $\sqrt{1-x^2}$ = tan^-1 $\frac{x}{\sqrt{1-x^2}}$ ; 0 < x < 1

cos^-1x = sin^-1 $\sqrt{1-x^2}$ = tan^-1 $\frac{\sqrt{1-x^2}}{x}$ ; 0 < x < 1

tan^-1x = cos^-1 $\frac{1}{\sqrt{1+x^2}}$ = sin^-1 $\frac{x}{\sqrt{1+x^2}}$ ; x > 0

tan^-1x + cot^-1x = $\frac{\pi}{2}$ ; $x \in R$

15) The solution of sin θ = 1 is $\left\{(4k+1)\frac{\pi}{2}/k\in Z\right\}$ ; [ i.e. P (B) = P ( 0, 1 ) ]

The solution of sinθ = –1 is $\left\{(4k-1)\frac{\pi}{2}/k\in Z\right\}$ ; [ i.e. P ( $B^\prime$ ) = P ( 0, –1 ) ]

The solution of cos θ = 1 is $\left \{ 2k\pi / k \in Z \right \}$ ; [ i.e. P (A) = P ( 1, 0 ) ]

The solution of cos θ = –1 is $\left \{ (2k \pm 1) \pi / k \in Z \right \}$ ; [ i.e. P ( $A^\prime$ ) = P (–1, 0) ]

16) The solution of cos θ = a, $\left|a\right| \le 1$ is $\left \{ 2k\pi\pm\alpha / \alpha = cos-1a, k \in Z \right \}$

The solution of sin θ = a, $\left|a\right| \le 1$ is $\left \{ k\pi + (-1)k\alpha / \alpha = sin-1a, k \in Z \right \}$

The solution of tan θ = a, $a \in R$ is $\left \{ k\pi + \alpha / \alpha = tan-1a, k \in Z \right \}$

17) The solution of a cos θ + b sin θ = c is { 2k π cos^-1 + α / k $\in$ Z }

Where, c² $\le$ r² and r² = a² + b²

α $\in$ [ 0, 2 π]

α is found from cos α = $\frac{a}{r}$ and sin α = $\frac{b}{r}$

18) Triangle, In-circle and Circum-circle :-

s = length of semi-perimeter of a triangle

= $\frac{a+b+c}{2}$

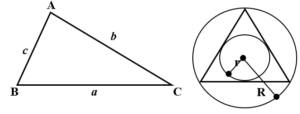
R = Circum-radius of a triangle

r = In-radius of a triangle

$\Delta$ = Area of a triangle

In $\Delta$ ABC,

( The length of an arc on unit circle corresponding to an angle is measured in radian )

Symbolically,m∠ BAC = A

m∠ ABC = B

m∠ BCA = C

BC = a

AC = b

AB = c

19) Sine – Rule :-

$\frac{a}{{sin}{A}} = \frac{b}{{sin}{B}} = \frac{c}{{sin}{C}} = 2R$

20) Cosine – Rule :-

cos A = $\frac{b^2+c^2-a^2}{2bc}$

cos B = $\frac{c^2+a^2-b^2}{2ca}$

cos C = $\frac{a^2+b^2-c^2}{2ab}$

21) The Projection Rule :-

a = b cos C + c cos B

b = c cos A + a cos C

c = a cos B + b cos A

22) Napier’s Formula :-

$tan\left(\frac{B-C}{2}\right)=\frac{b-c}{b+c} cot \frac{A}{2}$

$tan\left(\frac{C-A}{2}\right)=\frac{c-a}{c+a}cot \frac{B}{2}$

$tan\left(\frac{A-B}{2}\right) = \frac{a-b}{a+b}cot \frac{C}{2}$

23) Formulae for semi-angle ( Half-angle formulae ) :-

$sin \frac{A}{2} = \sqrt{\frac{(s-b)(s-c)}{bc}}$

$sin \frac{B}{2} = \sqrt{\frac{(s-c)(s-a)}{ca}}$

$sin \frac{C}{2} = \sqrt{\frac{(s-a)(s-b)}{ab}}$

$cos \frac{A}{2} = \sqrt{\frac{s(s-a)}{bc}}$

$cos \frac{B}{2} = \sqrt{\frac{s(s-b)}{ca}}$

$cos \frac{C}{2} = \sqrt{\frac{s(s-c)}{ab}}$

$tan \frac{A}{2} = \sqrt{\frac{(s-b)(s-c)}{s(s-a)}}$

$tan \frac{B}{2} = \sqrt{\frac{(s-c)(s-a)}{s(s-b)}}$

$tan \frac{C}{2} = \sqrt{\frac{(s-a)(s-b)}{s(s-c)}}$

24) The area of $\Delta$ ( The area of ABC ) :-

$\Delta = \frac{1}{2} bc \times sin A$

$\Delta = \frac{1}{2} ac \times sin B$

$\Delta = \frac{1}{2} ab \times sin C$

$\Delta = \sqrt{s(s-a)(s-b)(s-c)}$

$cot A = \frac{b^2+c^2-a^2}{4\Delta}$

$cot B = \frac{c^2+a^2-b^2}{4\Delta}$

$cot C = \frac{a^2+b^2-c^2}{4\Delta}$

$\Delta = \frac{abc}{4R}$

25) Formulae for In-radius :-

r = $\frac{\Delta}{s}$

r = $4R \ sin\frac{A}{2} sin\frac{B}{2} sin\frac{C}{2}$

r = $(s-a) \ tan \frac{A}{2} \Rightarrow cot \frac{A}{2} = \frac{s-a}{r}$

r = $(s-b) \ tan \frac{B}{2} cot \frac{B}{2}$ = $\frac{s-b}{r}$

r = $(s-c) \ tan \frac{C}{2} \Rightarrow$ $cot \frac{C}{2} = \frac{s-c}{r}$

26) In $\Delta$ ABC ( if A + B + C = $\pi$ ), then

sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C

sin² B + sin² C – sin² A = 2 sin B sin C cos A

cos A + cos B + cos C = 1 + 4 sin $\frac{A}{2}$ sin $\frac{B}{2}$ sin $\frac{C}{2}$

tan A + tan B + tan C = tan A tan B tan C

Click here to see Examples

Blog

Domain Range Co-domain Zeros and Principal Period of Trigo Functions : -

Leave a Reply Cancel reply