(1) The shadow of a building is 30m long when the angle of elevation of the sun is 60^o. Find the height of the building.

Soln. Let AB be the building and AC be its shadow.

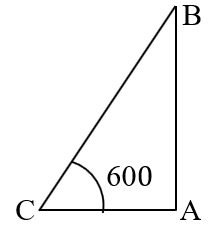
Then, AC  =  30m and  ∠ACB  =  60.

Let  AB  =  h.

Then,  =  tan 60  =

h  =  30   =  30 × 1.732  = 51.96 m

 (2) If a vertical pole  6 m high has a shadow of  length  6 meters, find the angle of elevation of the sun.

Soln. Let  AB be the vertical pole and AC be its shadow.

Let  the angle of elevation be  θ. Then,

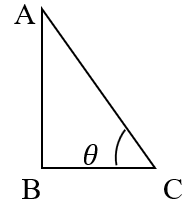
AB  =  6 m, AC  =  6 m and  ∠ACB  = θ.

Now,  tanθ =    =    =  tan 30    θ  =  30.

(3) The pilot of a helicopter, at an altitude of  1500 m finds that the two ships are sailing towards it in the same direction. The angles of depression of he ships an observed from the helicopter are 60^o and  45^o respectively. Find the distance between the two ships.

Soln. Let  B  be the position of the helicopter and let C, D be the ships. Let AB be the vertical height.

Then, AB  =  1500m, ∠ACB  =  60^o  &

∠ ADB  =  45.

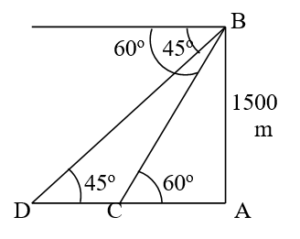
Now, in  Δ ABD,

tan  45  =    =  1

⇒   =  1  ⇒  AD  =  1500m

 ↦ Now, in  Δ ABC,

tan  60⁰   =     = 

Distance between the ships

=  CD  =  AD – AC

=  ( 1500 – 500 ) m

=  ( 1500 – 500 × 1.732 ) m

=   634 m.

(4) A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height  10 m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30^o and that of the top of the flagstaff is  45^o.  Find the height of the tower.

Soln. Let  AB be the tower and  BC be the  flagstaff. Then, BC  =  10 m. Let AB  =  h.

Let  O  be the point of observation.

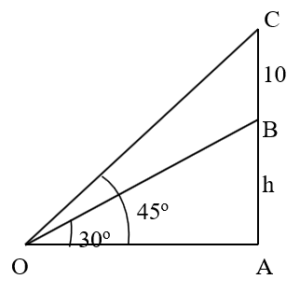
Then, ∠AOB  =  30^o  and  ∠AOC  =  45^o.

↦ Now,  in ∠AOC,    tan 45 =  =  1

  OA  =  AC  =  h + 10.

↦ Now,  in ∠AOB,    tan 30 =

   =    =    13.66  m.

Best of Luck…