Blog
Concept of Congruent and Similar
- August 7, 2020
- Category: Concept of Congruent and Similar
☼ Concept of Congruent and Similar :–
■ Congruent Figures : –
Figures having the same shape, same measures and same areas are called congruent figures.

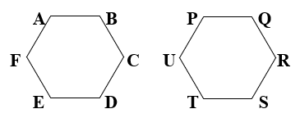
- Above two circles are congruent. Above two hexagons are also congruent.
■ Similar Figures : –
Figures having the same shape but different measures and different areas are called similar figures.
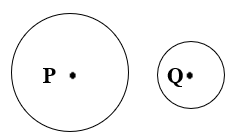


- Above two circles are similar. Above two hexagons are also similar. Also above two triangles.
■ Congruent Triangles :-
For a correspondence of two triangles, if the corresponding angles and measures of corresponding sides are congruent then this correspondence is called congruent.
In this case, those two triangles are called congruent triangle.


Here for ABC &
PQR ,
mA = m
P, m
B = m
Q, m
C = m
R
&
AB = PQ , BC = QR , AC = PR
ABC
PQR OR Correspondence ABC
PQR is congruent.
SAS Postulate :-
For a correspondence of two triangles, if two sides and the included angle of the one triangle is congruent to the corresponding two sides and included angle of the other triangle, then given two triangles are congruent.

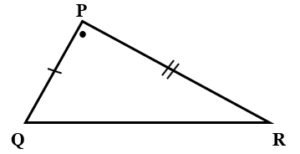
e.g. Here,
AB = PQ , mA = m
P, AC = PR
ABC
PQR
SAA Postulate :-
For the correspondence of two triangles, if two angles and a side of the one triangle are congruent to the corresponding two angles and a side of the other triangle, then given two triangles are congruent.

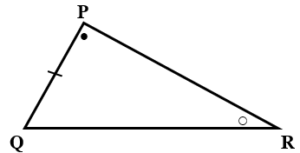
e.g. Here,
AB = PQ , mA = m
P, m
C = m
R
ABC
PQR
ASA Postulate :-
For the correspondence of two triangles, if two angles and included side of the first triangle are congruent to the corresponding two angles and included side of the other triangle, then given two triangles are congruent.

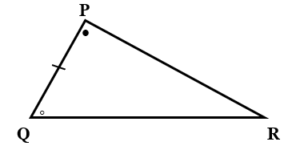
e.g. Here,
mA = m
P, AB = PQ , m
B = m
Q
ABC
PQR
SSS Postulate :-
For the correspondence of two triangles, if the measures of corresponding sides are congruent then this correspondence is called congruent.

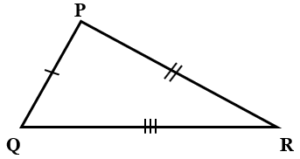
e.g. Here,
AB = PQ , BC = QR , AC = PR
ABC
PQR
RHS Theorem :-
For a correspondence of two right angled triangle, if one side and hypotenuse is congruent to corresponding side and hypotenuse then that correspondence is called RHS and from these we gent two congruent triangles.


e.g. Here,
AB = PQ , mB = m
Q = 900, AC = PR
ABC
PQR
■ Similar Triangles :-
For a correspondence of two triangles, if the corresponding angles are congruent and the measures of the corresponding sides are in the same proportion, then this correspondence is called a similarity.


e.g. Here for ABC &
PQR ,
mA = m
P, m
B = m
Q, m
C = m
R
&
ABC ~
PQR OR Correspondence ABC
PQR is similarity.
AA Postulate :-
If for any correspondence between two triangles two pairs of corresponding angles are congruent, then the correspondence is similarity.

e.g. Here for ABC &
PQR ,
mA = m
P, m
B = m
Q
ABC ~
PQR OR Correspondence ABC
PQR is similarity.
SAS Theorem :-
If for a correspondence between two triangles, two pairs of corresponding sides are proportional and the included angles are congruent, then the correspondence is a similarity.

e.g. Here for ABC &
PQR ,
, m
A = m
P
ABC ~
PQR OR Correspondence ABC
PQR is similarity.
SSS Theorem :-
For a given correspondence of two triangles, if the corresponding sides are in proportion, then the correspondence is a similarity.

e.g. Here for ABC &
PQR ,
ABC ~
PQR
SSS Theorem :-
For a given correspondence of two triangles, if the corresponding sides are in proportion, then the correspondence is a similarity.
RHSI Theorem :-
For a given correspondence of two right angled triangle, if hypotenuse and one of the sides of a triangle is proportion to that of other triangle then the given correspondence is similar.


e.g. Here for ABC &
PQR ,
, m
B = m
Q = 900
ABC ~
PQR
■ Formula Based on Similarity of Triangle :–
If ABC ~
PQR, then
=
=
=
=
.
( Where, ABC = Perimeter of
ABC. )
And =
=
=
=
.
( Where, ABC = = Area of
ABC. )
Also, Altitudes
Angle Bisectors
Medians

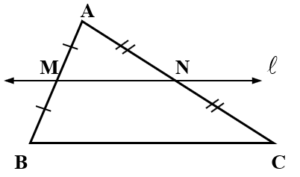
If
is parallel to
of
ABC, then
*
*
*

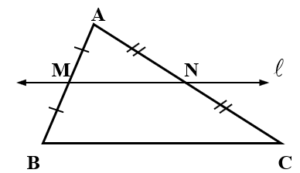
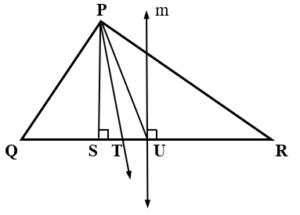
In
ABC, G is the centroid and line l and through G is parallel to
and intersect
in M and
in N, then
*
*
*

In
ABC, line l is parallel to
and intersect
and
in their respective mid–points, namely M and N, then
*
*
*
In
ABC, medians
and
intersect at G such that
║
and K
, then
AC = 6 EK

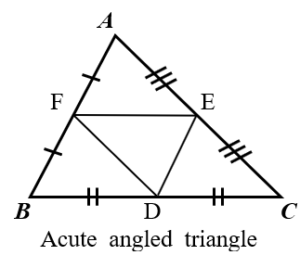
In
ABC, D, E and F are respectively the mid–points of
and
. Then
ABC = 4 DEF
&
ADF = DBE = FBC = EFD
( Always Remember, ABC = = Area of
ABC &
ABC = Perimeter of
ABC . )
If in
ABC,
is produced to D, then m
ACD = m
A + m
B.
In this case, mACD is called the exterior angle of
ABC. And
A and
C are opposite interior angles of m
ACD.
i.e. Exterior angle = Sum of its opposite interior angles

In
ABC, if
is the bisector of
BAC and
, then
m MAN =
( m
B – m
C )
Pythagoras’ Law :
In a right angled ABC, if mB is a right angle, then

AB2 + BC2 = AC2
or
AC2 = AB2 + BC2
Some of the Pythagorean triplets are:
( 3, 4, 5 ); ( 5, 12, 13 ); ( 7, 24, 25 ); (8, 15, 17 ); ( 9, 40, 41 ); ( 11, 60, 61 );
( 12, 35, 37 ); ( 16, 63, 65 ), ( 20, 21, 29 )
In an acute angled
ABC, if m
B is an acute angle, then
AC2 < AB2 + BC2
In an obtuse angled
ABC, if m
B is an obtuse angle, then
AC2 > AB2 + BC2

In an acute angled
ABC, if m
B is an acute angle, then
AC2 = AB2 + BC2 – 2BC • BM

In an obtuse angled ABC, if mB is an obtuse angle, then
AC2 = AB2 + BC2 + 2BC • BM

In a right angled ABC, if mB is a right angle, then
* BM2 = AM CM
* AB2 = AM AC
* BC2 = CM AC

If line l passes through the mid–points M and N of
and
respectively, then l ║
& MN =
BC