☼ Event     :     The result  of  an  experiment  are  known as events:

e.g. (i) If a coin is tossed head ( H ) and tail ( T ) are two different events.

(ii) 1, 2, 3, 4, 5, 6 are different events when a die is thrown.

 If A is an event and S is a sample space then A  is a subset of  S. ( i.e. A  S )

 Generally the events are denoted by A, B, C  or  A₁,  A_2,  A₃ etc.

   If  A  = ,  then A is called impossible event.

   If  A  =  S,  then  A is called certain ( or  sure ) event.

■ Complementary  event    :     The complement of an event A is the aggregate of  all the sample points of  sample space S which do not belong to A. It is denoted by A’ or   or  A .

e.g.   If  A is an event of getting an odd number when a die is thrown, then event of not getting an odd number i.e. getting an even number is the complement of  event A and it is denoted by A’ or or  .

■  Union  of  two  events    :    The union of two events A and B is denoted by  A  B. It is the aggregate of all sample points belonging to either A or B or both.

e.g.    If A is an event that no. of  students play cricket and B is an event that no. of  students play hockey  then  A  B  represents an event that no. of  students play either cricket or hockey or both.

■  Intersection  of  two  events    :     The intersection two events A and B is denoted by A  B. It is the aggregate of  all sample points belonging to A and B both. When two events A and B occur simultaneously we say that A  B has occurred.

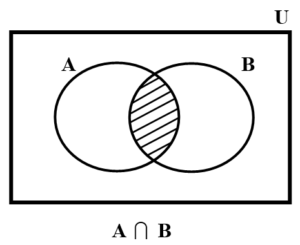
e.g.      If A is an event that no. of  students play cricket and B is an event that no. of  students play hockey, then  A  B represents an event that no. of  students play cricket and hockey both.

■ Difference  of   events    :     The difference of two events A  and  B  is the event that A happens and B does not happen. It is denoted by A – B.       A – B   =   A B’

e.g.        If  A is an event that a student plays cricket and B is an event that a student plays hockey, then  A – B denotes an event that a student plays only cricket.

■  Mutually  exclusive   events    :     The intersection of two events A  and  B  is null set, then they are called mutually exclusive events.    i.e.  A  B   = 

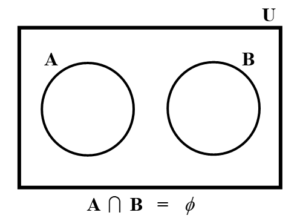
e.g. If  A is an event that a student pass in the exam and B is an event that a student fail in the exam, then  A and B are called mutually exclusive events.

■ Exhaustive   events    :    If all possible outcomes of  an experiment are considered, the outcomes are said to be exhaustive. The exhaustive events are nothing but all the sample points in the sample space.

 e.g. In throwing a die 1, 2, 3, 4, 5, 6  are exhaustive events.

■ Equally   likely   events    :   Events are said to be equally likely if  we have no reason to believe that one event is preferable to the others.

 e.g. Head  ( H )  and  Tail  ( T )  are equally likely events in tossing a coin.

■ Favourable   cases    :   The number of sample points favourable to the happening of an event A are known as favourable cases of A

 e.g. In  drawing  a  card  from  a  pack  of  52  cards,  the   favourable  cases  for  getting.

■ Independent events   :  Events are said to be independent if the happening of one event does not depend upon the happening or non-happening of other events.

e.g. (i) When a coin  is  tossing two times, the event  of  getting  head  in the first throw and  that of  getting head in the second throw are  independent events.  Here the result of the  second  throw does not  depend upon the result of  the first throw.

(ii) Similarly the event of getting 3 when a die is thrown and getting a spade from a pack of cards are independent events.

Click to next