(21) What least number must be added  and subtract to 3000 to obtain a number exactly divisible by 19 ?

Soln. On dividing 3000 by 19, we get 17 as  a  remainder.

∴ Number to be added

=   ( 19 – 17 )

=   2

&  Number to be subtracted

=  17

(22) Find the number which is nearest  to 3115 and is exactly divisible by 23.

Soln. On dividing  3105  by  23,  we get  10  as  a  remainder.

∴ Number to be added

=   ( 23 – 10 )

=   13

&  Number to be subtracted

=  10

Hence, required nearest  number  =  3115 – 10  =  3105.

(23) A number when divided by 437 gives a remainder 47.  When the same number is divided by  19, what would be the remainder ?

Soln.

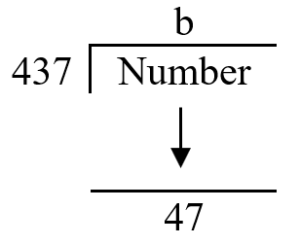
The easiest value of

b is 0.

∴ We get,

Number  =  47

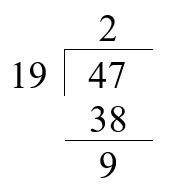
∴ On  dividing  47  by  19  we  get  the  remainder  9.

 (24) A number being successively divided by  3,  5  and  8  leaves remainders  1, 4  and  7  respectively. Find the respective remainders if the order of  divisors be reversed.

Soln.

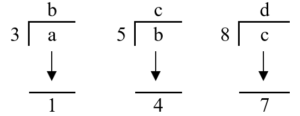
Soln. Let  d  =  0,  then  c

=   8 × 0 + 7

=   7

Now,  b

=    5 × 7  +  4    =    39

And    a

=    3 × 39  + 1   =   118

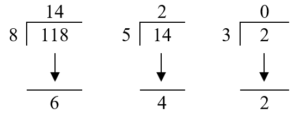
Hence,  that  number   =   118.     &      Now,

∴  Respective  remainders  are  6,  4,  2.

(25) How many numbers between  20  and  100  are divisible by 7 ?

Soln. The required numbers are  21, 28, 35, …, 98.

∴   =  7n + 14  ⇒  7n + 14  =  98

∴  n  =  12

Click here to see more examples