1) Δ PQR  is an equilateral triangle.  Find  QSR  and  QTR.

Soln. Δ PQR  is equilateral.   ∴ ∠QPR  =  60⁰.

∴∠QSP  =  60⁰

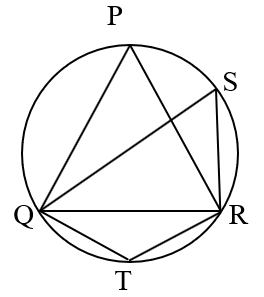
(  ∵ Angles subtended on the same side of the chord on the circle )

∠ QTR + ∠QSP  =  180⁰

( ∵ QSRT is cyclic quadrilateral )

∴∠QTR  =  120⁰.

(2)  ABCD is a cyclic quadrilateral whose side AB is a diameter of  the circle through A, B, C and D.  If  ADC  =  130^o, find BAC.

Soln.

In  ABC,  ∠C  =  90⁰.

∠ADC + ∠CBA = 180⁰   ( ∵ ABCD is cyclic )

∴∠CBA  =  50⁰.

∠CAB  =  180⁰ – ( 90⁰ + 50⁰ )

(  ∵ Δ ABC is a triangle. Hence, sum of  angles  =  180^o )

=  180⁰ – 140⁰  =  40⁰.

(3)  Given  PA  =  4, AB  =  5. Find  PT.

Soln.

PA  =  4  and  AB = 5  ⇒ PB =  PA + AB = 4 + 5 = 9

Now, 

PT²  =  PA × PB  =   4 × 9  =  36

∴   PT     =     6

(4)  Find  x.

Soln.

5 × 6  =  3 × x

∴   x  =  10.

Best of Luck…