☼    LINES   ☼

☼ Cramer’s  Rules  :  

  If  l₁  :  a₁x   +  b₁y  +  c₁  =  0

and  l₂ :   a₂x  +  b₂y  +  c₂  =  0

( Where, a_i,  b_i,  c_i  are  real numbers  and   :  i = 1, 2 )

 (i) Intersecting  Lines :–   If  ,  then  lines l₁ and l₂ are intersecting.

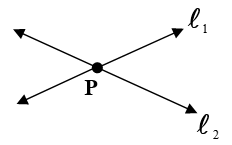
In  this  case,  we  get  the  unique  solution ( say point P ).

                This unique solution,  P  = 

 (ii) Parallel  Lines :–   If  ,  then  lines  l₁  and  l₂ are  parallel.

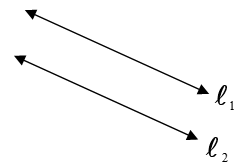
In  this  case,  we  get  the  no  solution.

i.e.    The  Solution  Set   = 

(iii) Identical  Lines :–   If  ,  then  lines l₁ and l₂ are  identical.

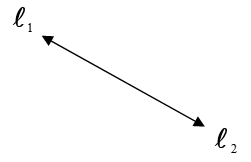
In  this  case,  we  get  infinite  solutions.

  i.e.    The  Solution  Set   =  { ( x, y )  /  a₁x   +  b₁y  +  c₁  =  0 :  x, y  R }

Click here to see next topic