☼ Some Special Type of Centers  :–

■ Altitude  &  Orthocenter :-  The three altitudes of a triangle are concurrent. The point of concurrence of the altitudes of a triangle is called the orthocenter of the triangle

The orthocenter is denoted by H.

Here,

mBHC  =  180⁰  –   mA

mAHC  =  180⁰  –   mB

mAHB  =  180⁰  –   mC

Orthocenter ( H )  : –

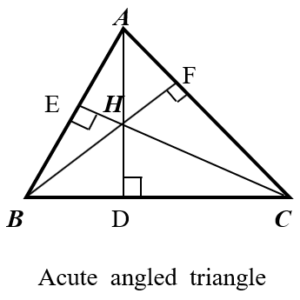
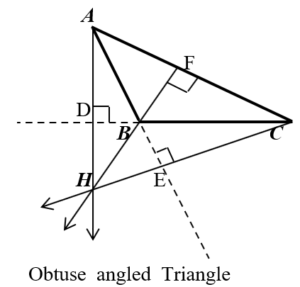
*  In an acute angled triangle the orthocenter lies inside the triangle.

*  In a right angled triangle the orthocenter lies on the right angle.

*  In an obtuse angled triangle the orthocenter lies outside the triangle.

■ Angle bisector & In-centre :-  The three angle- bisectors of a triangle are concurrent. The point of concurrence of the angle bisectors of a triangle is called  the  In-centre  of  the  triangle.

The in-centre is denoted by I.

Here,

  &     & 

mBIC   =    90⁰  –   mA

mAIC   =    90⁰  –   mB

mAIB   =    90⁰  –   mC

Incentre ( I )  : –

* In any triangle the incetre lies inside the triangle.

* I is the centre of incircle  ( the circle touches all the three sides ) of the triangle.

* The radius of incircle is denoted by  r.

■ Median & Centroid   :-      The three medians of a triangle are concurrent. The point of concurrence of medians of a triangle is called Centroid of the triangle.

* The centroid is denoted by  G.

* Here,

  &

  &

Centroid ( G )  : –

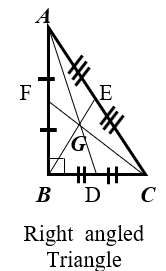
* In any triangle the centroid lies inside the triangle.

* G divides the median from the vertex in the ratio 2 : 1

■ Perpendicular  bisector  and  Circumcentre  :-   The perpendicular bisector of a triangle are concurrent. The point of concurrence of the perpendicular bisectors of a triangle is called circumcentre of a triangle.

* The circumcentre of a triangle is denoted by P.

* Here,

mBPC  =  2 mA

mAPC  =  2 mB

mAPB  =  2 mC

Circumcentre ( P )  : –

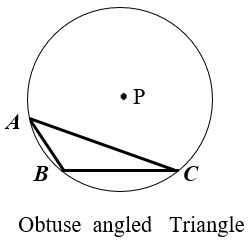
*  In an acute angled triangle circumcentre lies inside the triangle.

*  In a right angled triangle circumcentre is the mid-point of hypotenuse.

*  In an obtuse angled triangle circumcentre lies outside the triangle.

■ Situation of all the four centres with respect to the various Triangles :–

* In a scalene triangle, all the four centres are non-collinear.

* In an isosceles triangle, all the four centres are collinear.

* In an Equilateral triangle, all the four centres are coincident ( i.e. on the same   point).

* G always divides  internally, in the ratio 2 : 1 from P.

Click here to next topic