Blog

Parin Sir > Quantitative Aptitude (Maths) > H. C. F. & L. C. M. OF NUMBERS > To find H.C.F. of Given Numbers > To find H.C.F. of Given Numbers

To find H.C.F. of Given Numbers

June 1, 2020
Category: To find H.C.F. of Given Numbers

No Comments

☼ To find H.C.F. of Given Numbers :

■ H. C. F. by Definition : Write all the factors (divisors) of each number and take common factors (divisors) of all factors (divisors) and then select the highest the factors (divisors) among them. This highest common factor is called the H. C. F.

e.g. Find the H.C.F. of 210, 126 and 84.

Soln. The factors (divisors) of given numbers are as follows

210 $\large \rightarrow$ 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210

126 $\large \rightarrow$ 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126

84 $\large \rightarrow$ 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84

$\therefore$ the common factors (divisors) of given numbers are :

1, 2, 3, 6, 7, 14, 21, 42,

And among above, the highest common factor is 42.

i.e. H. C. F. = 42.

Hence, (210, 126, 84) = 42.

If a is any positive integer, then it can be written as in the product of prime numbers.

i.e. a = $p_{1}^{x} \times p_{2}^{y} \times ... \times p_{n}^{z}$ ( Where, $p_{1},p_{2},...p_{n}$ are distinct primes.)

Then number of factors of a = (x + 1) · (y + 1) · . . . · (z + 1)

[ e.g. 126 = $2 \times 3^{2} \times 7$

= $2^{1} \times 3^{2} \times 7^{1}$

Number of factors of 126 = (1 + 1) · (2 + 1) · (1 + 1)

= 2 $\times$ 3 $\times$ 2

= 12

■ H.C.F. by Factorization in the form of multiplication : Express each number as the product of primes. Now, take the common factors to get the H.C.F.

e.g. Find the H.C.F. of 99000, 220500 and 2102100.

Soln. 99000 = 2 $\times$ 2 $\times$ 2 $\times$ 3 $\times$ 3 $\times$ 5 $\times$ 5 $\times$ 5 $\times$ 11

220500 = 2 $\times$ 2 $\times$ 3 $\times$ 3 $\times$ 5 $\times$ 5 $\times$ 5 $\times$ 7 $\times$ 7

2102100 = 2 $\times$ 2 $\times$ 3 $\times$ 5 $\times$ 5 $\times$ 7 $\times$ 7 $\times$ 11 $\times$ 13

Taking the common factors, we get :

H.C.F. = 2 $\times$ 2 $\times$ 3 $\times$ 5 $\times$ 5

= 300

Hence, (99000, 220500, 2102100) = 300.

■ H.C.F. by Factorization in the form of powers : Express each number as the product of primes. Now, take the product of least powers of common factors to get the H.C.F.

e.g. Find the H.C.F. of 448, 792 and 1056.

Soln. We have :

448 = $2^{6}$ $\times$ 7

792 = $2^{3}$ $\times$ $3^{2}$ $\times$ 11 and

1056 = $2^{5}$ $\times$ 3 $\times$ 11

Taking the product of least powers of common factors, we get :

H.C.F. = $2^{3}$ = 8.

Hence, ( 448, 792, 1056 ) = 8.

■ H.C.F. from the method of L. C. M. : Arrange the given numbers in a row in any order. Divide by a number which divides exactly at least two of the given numbers and carry forward the numbers which are not divisible. Repeat the above process till no two of the numbers are divisible by the same number expect 1. The product of the common divisors are called H. C. F. of the given numbers.

e.g. Find the L.C.M. of 48, 24, 36 and 54.

Solution:

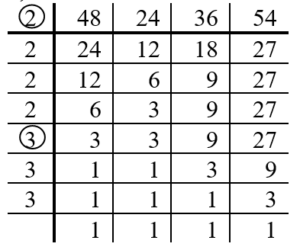
C. F. = 2 $\times$ 3 = 6.

Hence, ( 48, 24, 36, 54 ) = 6.

■ H.C.F. By Division ( Division Algorithm ) : Divide larger number by smaller one. Now, divide the divisor by the reminder. Repeat the process of dividing the preceding divisor by the remainder last obtained, till the remainder ‘0’ is obtained. The last divisor is the required H.C.F.

▪ Suppose we have to find the H.C.F. of three numbers, the H.C.F. of (H.C.F. of any two and the third number) gives the H.C.F. of given three numbers.

e.g. Find the H.C.F. of 384 and 528.

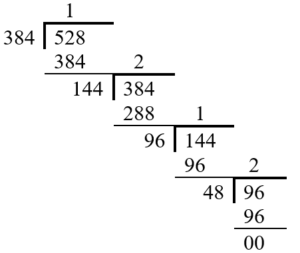
$\therefore$ H.C.F. of given numbers = 48.

▪ Finding the H.C.F. of more than two numbers : Suppose we have to find the H.C.F. of three numbers, Then H.C.F. of [(H.C.F. of any two) and (the third number)] gives the H.C.F. of three numbers.

Similarly, the H.C.F. of more than three numbers may be obtained.

e.g. Find the H.C.F. of 204, 340 and 425

Soln. By division method, we can find that:

H.C.F. of 204 and 340 = 68.

H.C.F. of 68 and 425 = 17.

H.C.F. of 204, 340 and 425 = 17.

i.e. ( 204, 340, 425 ) = 17

e.g. Reduce $\frac{1053}{1209}$ to lowest terms.

Soln. H.C.F. of 1053 & 1209 is 39.

On dividing Numerator & Denominator of the given fraction by 39, we get :

$\frac{1053}{1209}$ = $\frac{27}{31}$ .

Click here to see next topic

Blog

To find H.C.F. of Given Numbers

Leave a Reply Cancel reply